Big O notation 예시 위주 정리

https://www.google.com/url?sa=i&url=https%3A%2F%2Fwww.youtube.com%2Fwatch%3Fv%3D47GRtdHOKMg&psig=AOvVaw0Vk1aDONHvIq3__7-l42ax&ust=1664940355444000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCJiWqanQxfoCFQAAAAAdAAAAABAD

 

 

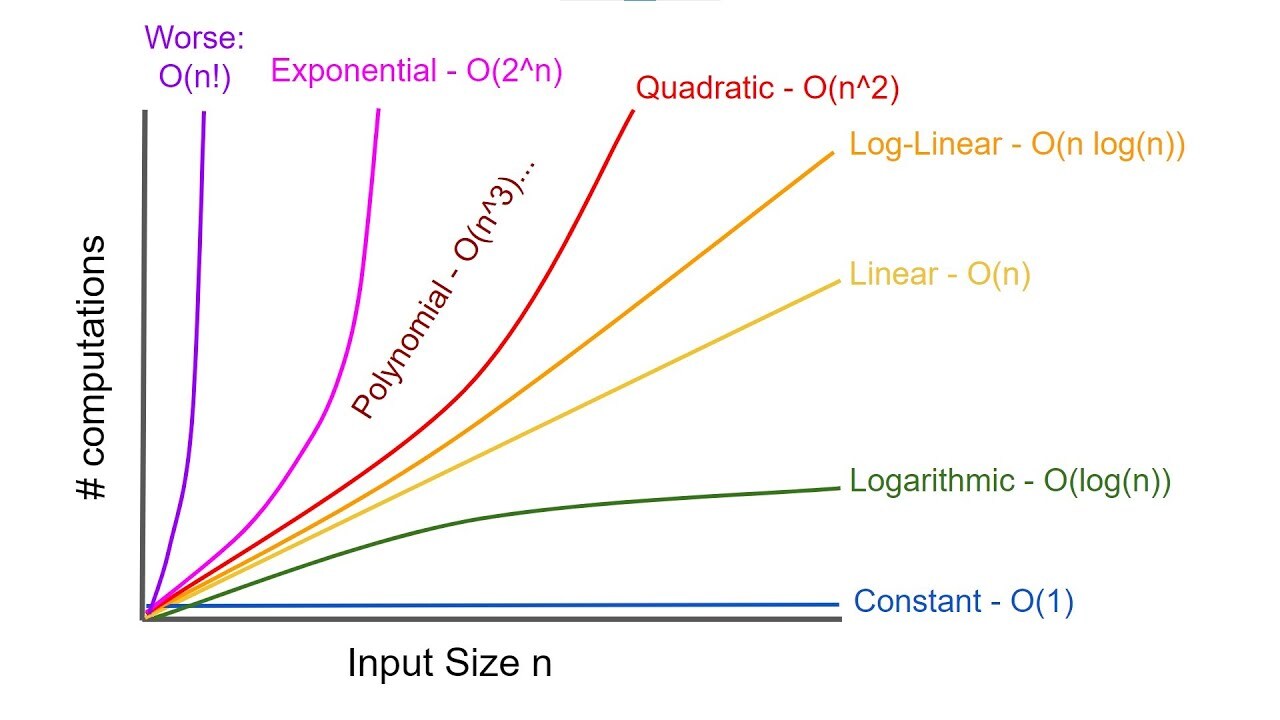
😎 Time Complexity  계산법

 

n이 input하는 변수의 사이즈(샘플값)이라고 할 때, 전체 시간 T를 아래와 같이 나타냅니다

 

T = an + b

1. find the fastest growing term

가장 차수가 큰 항을 찾는다

-> fastest going term is 'an'

2. take out the coefficient

앞에 상수를 제외 한다

-> O(n)

 

예시) 

T = cn**2 + dn + e

1. cn**2

2. n**2 -> O(n**2)



T = c

1. c

2. 1 -> O(1)

---

O(1) Constant time 예시)

 

def function(array):

    total = 0             -> O(1)

    return total        -> O(1)



T = O(1) + O(1) = c1 + c2 = c3 = O(1)

 

---

O(n) Linear time 예시)

 

def function(array):

    total = 0             -> O(1)

    for each i in array:

          total += i     -> O(1)

    return total        -> O(1)



T = O(1) + n*O(1) + O(1)

= c4 + n*c5 = O(n)

 

---

O(n**2) Quadratic time 예시)

 

array_2d = [[1,4,3,1],[3,1,9,4],[0,5,2,6],[4,5,7,9]]

행 수 = 열 수 = n으로 가정할 때 전체 합을 구하는 함수를 다음과 같이 가정함

 

def find_sum(array):

    total = 0                                        -> O(1)

    for each row in array_2d:

              for each i in row:

                      total += i                   -> O(1)

return total                                      -> O(1)

 

T = O(1) + n^2*O(1) + O(1)

=  O(n**2)

 

O(2*n^2) = O(n^2)

T = 2*n^2 + c*n + c

= (2c) * n^2 +cn + 3

 

https://www.google.com/url?sa=i&url=https%3A%2F%2Flevelup.gitconnected.com%2Ftime-and-space-complexity-725dcba31902&psig=AOvVaw3n4PIMguLSEUTqIpK8jM_-&ust=1664947229497000&source=images&cd=vfe&ved=0CAwQjRxqFwoTCPi75JPqxfoCFQAAAAAdAAAAABAD

 

 

 

O(log n) 예시_)

function logn(n) {
	while (n>1) {
    n = math.floor(n/2)
    }
 }

iteration1 : n = 8/2 = 4

iteration2: n = 4/2 = 2

iteration3 : n = 2/2 = 1

 

O(log8) = 2**? = 8

여기서 중요한건 2가 로그 밑일 때 반복되는 계산 횟수인 3으로 O(logn) 이 됨

 

 

Binary Search & O(logn)

 

Source: stackoverflow

 

 

 

전체 binary search의 분류가 b 사이즈로 x번 갈라지는지를 n/b^x = 1 로 생각했을 때,

n = b^x 이면 x = logn/logb 가 됩니다

 

이진분류로 b가 2이기 때문에 결론적으로 binary search의 Time complexity 는 O(logn)이 되는거죠

 

 

 

https://medium.com/@jacolam/binary-searches-9f0e90e52eff

 

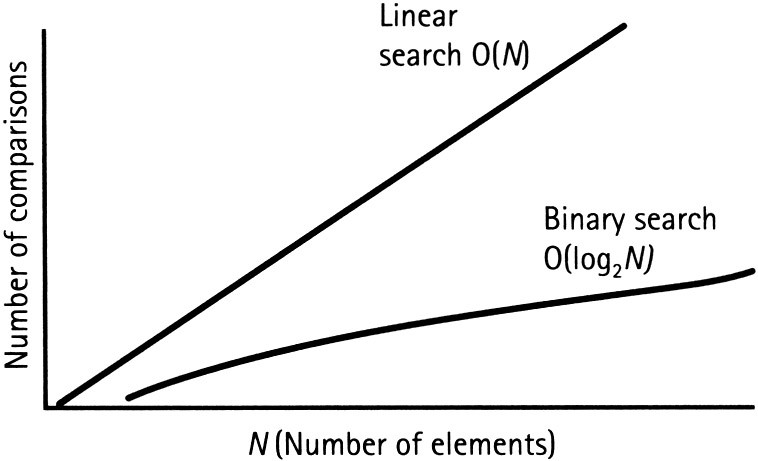
그래프만 봐도 일반적인 O(n)보다 Binary search가 훨씬 빠른 것을 알 수 있습니다

 

O(nlogn)

function nLogNFunc(n) {
    let y = n;
    while (n>1) {
        n = math.floor(n/2);
        for (let i=1;i<=y;i++) {
        	console.log(i)
        }
     }
   }

 

Merge sort & O(nlogn) 

Source: Geeksforgeeks

 

 

Merge sort의 과정은 위 사진부터 계속해서 반으로 자르는 과정 => O(logn) 을 거치고 

쪼개어진 부분들을 다시 merge 해서 정렬하는 과정을 거칩니다

 

여기서 merge 를 하기 위해서는 쪼개진 부분들을 다시 순회해야 합니다.

때문에, 전체 n *logn => O(nlogn)만큼의 Time complexity를 거치게 됩니다

 

 

가장 많이 하는 실수

 

1. 2개의 for 문 반복 시 O(2n) = O(n)과 O(n**2) 의 혼동

 

아래 사례는 a라는 input에 대한 for 문이 2개로 O(n+n) = O(2n) = O(n)

Source: Selikapro

 

반면, 아래는 a와 b의 사이즈를 알 수 없으므로 각각 추적해야 하므로 O(a+b)

 

Source: Selikapro

 

twoInputMult는 O(n**2)로 혼동하기 쉽지만, 위와 마찬가지로 a,b는 사이즈가 같을 수도, 다를 수도 있는

별개로 계산해야 하기 때문에 time complexity는 O(a*b)가 됨

 

 

Source:

https://www.youtube.com/watch?v=Mo4vesaut8g&t=454s&ab_channel=freeCodeCamp.org