코딩문제에 단골로 등장하는 Dynamic Programming에 대해 더 알아보기 위해 공부한 유투브 동영상을 정리해봤습니다
https://www.youtube.com/watch?v=aPQY__2H3tE&t=10s&ab_channel=Reducible
Dynamic Programming 이란?
- 부분문제(subproblem)을 식별하고 해결해서 큰 문제를 해결하는 방식
[ 5 Steps to solve DP ]
1. Longest Increasing Subsequence (LIS)
문제 정의하고 살펴보기
a1에서 a(n)까지 [3,1,8,2,5]가 있을 때, 1,2,5는 연속되면서 계속 증가하는 Subsequence 중에서 3개로 가장 긴 길이에 해당
2. Visualize Examples => Draw Acyclic directed Graph
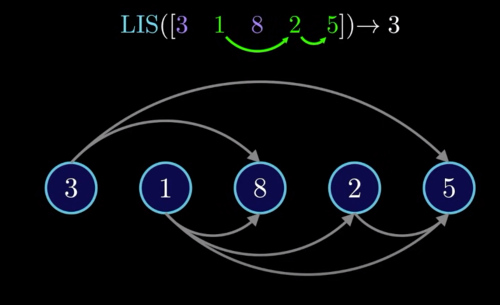
- LIS = Longest Path in DAG + 1
- 노드의 개수 -> path의 개수 + 1
3. Find an appropriate subproblem
- All increasing subsequences are subsets of original sequence
- All increasing subsequences have a start and end
- Focus on the end index of an increasing subsequence is more intuitive
Subproblem: LIS[k] = LIS ending at index k
LIS[4] = 1 + max{LIS[0], LIS[1],LIS[3]}
4. Generalize the relationship
LIS[n] = 1 + max{LIS[k] | k < n, A[k] < A[n]}
5. Implement by solving subproblems in order
순방향, 역방향, 오름차순, 내림차순으로 전개해야 하는지 파악하기

여기서 Sequence를 얻는 방법은?
i 라는 index 값의 이전 sequence 값 = 이전 sequence 값이 위치한 index j ==> prev[i] = j로 표현 가능함
Box Stacking
(길이 L, 가로 W, 세로 H)인 n 개의 상자 리스트가 주어졌을 때, 가장 높이가 높은 stack을 찾으시오
위의 법칙을 단계별로 따라보자면,
시각화해서 생각하기)
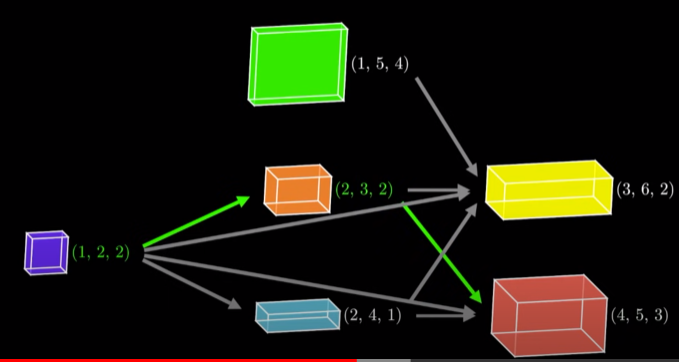
Subproblem ) 가장 높은 height는 밑에 쌓은 box의 합에 해당함
예를 들어 , height(4,5,3)이 밑에 가는 box stack의 높이는
height(2,3,2) = 4 , height(2,4,1) = 3, height(1,2,2) = 2
==> 즉 height(4,5,3) = 3 + max{height(2,3,2), height(2,4,1),height(1,2,2)}
일반화 )
1. 박스위에 쌓여질 수 있는 box를 구한다
2. 그 중에서 최대 높이를 가장 아래 박스의 높이에 더한다
순서 정하기 )

동영상을 보면 기본적인 전개 과정은 이해가 가지만, 막상 문제상황에 닥쳤을 때
subproblem을 정하고 코드로 옮기기 까지 많은 연습이 필요한 것 같습니다!
'Data Structure & Algorithm' 카테고리의 다른 글
| Trie (트라이, Digital tree, prefix, Retrieval tree) + 예제 코드 (0) | 2022.09.27 |
|---|---|
| Union Find (0) | 2022.09.26 |
| Stack & Queue 개념 정리 (0) | 2022.09.21 |
| Singly & Doubly Linked List (0) | 2022.09.20 |
| Big O notation & Array (0) | 2022.09.19 |




댓글